Trigonometrik funksiyalarning integrasiyasi. Trigonometrik funksiyalarni integrallash: trigonometrik integrallarni yechish usullari va misollar.

Asosiy trigonometrik formulalar va asosiy almashtirishlar keltirilgan. Trigonometrik funktsiyalarni integrallash usullari ko'rsatilgan - ratsional funktsiyalarning integrasiyasi, sin x va cos x darajali funktsiyalarining mahsuloti, ko'p nomli, ko'rsatkichli va sinus yoki kosinusning mahsuloti, teskari trigonometrik funktsiyalarning integrasiyasi. Nostandart usullar ta'sir qiladi.

Tarkib

Trigonometrik funksiyalarni integrallashning standart usullari

Umumiy yondashuv

Birinchidan, agar kerak bo'lsa, integral trigonometrik funktsiyalar integratsiya o'zgaruvchisi bilan bir xil bo'lgan bitta argumentga bog'liq bo'lishi uchun o'zgartirilishi kerak.

Misol uchun, agar integral bog'liq bo'lsa gunoh(x+a) Va cos(x+b), keyin konvertatsiyani amalga oshirishingiz kerak:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + gunoh ( x+a ) gunoh (b-a).
Keyin z = x+a almashtiring. Natijada trigonometrik funksiyalar faqat z integrasiya o‘zgaruvchisiga bog‘liq bo‘ladi.

Trigonometrik funksiyalar integrasiya o‘zgaruvchisiga (deylik, z) to‘g‘ri keladigan bitta argumentga bog‘liq bo‘lsa, ya’ni integrand faqat quyidagi kabi funksiyalardan iborat bo‘ladi: gunoh z, cos z, tg z, ctg z, keyin almashtirishni amalga oshirishingiz kerak
.
Bunday almashtirish ratsional yoki irratsional funktsiyalarni (agar ildizlar mavjud bo'lsa) integrallashiga olib keladi va elementar funktsiyalarda integrallashgan bo'lsa, integralni hisoblash imkonini beradi.

Biroq, ko'pincha integralning o'ziga xos xususiyatlaridan kelib chiqqan holda, integralni qisqaroq tarzda baholashga imkon beradigan boshqa usullarni topishingiz mumkin. Quyida bunday asosiy usullarning qisqacha tavsifi keltirilgan.

sin x va cos x ning ratsional funksiyalarini integrallash usullari

dan ratsional funktsiyalar gunoh x Va chunki x dan tuzilgan funksiyalardir gunoh x, chunki x va qo‘shish, ayirish, ko‘paytirish, bo‘lish va butun son darajaga ko‘tarish amallari yordamida har qanday konstantalar. Ular quyidagicha belgilanadi: R (sin x, cos x). Bunga tangentlar va kotangentlar ham kirishi mumkin, chunki ular sinusni kosinusga va aksincha bo'lish orqali hosil bo'ladi.
Ratsional funktsiyalarning integrallari quyidagi ko'rinishga ega:
.

Ratsional trigonometrik funksiyalarni integrallash usullari quyidagilardan iborat.
1) almashtirish har doim ratsional kasrning integraliga olib keladi. Biroq, ba'zi hollarda, qisqaroq hisob-kitoblarga olib keladigan almashtirishlar mavjud (bular quyida keltirilgan).
2) Agar R (sin x, cos x) cos x → - cos x gunoh x.
3) Agar R (sin x, cos x) almashtirishda -1 ga ko'paytiriladi sin x → - sin x, keyin almashtirish t = chunki x.
4) Agar R (sin x, cos x) bir vaqtning o'zida almashtirish kabi o'zgarmaydi cos x → - cos x, Va sin x → - sin x, keyin almashtirish t = tg x yoki t = ctg x.

Misollar:
, , .

cos x va sin x ning daraja funksiyalarining mahsuloti

Shaklning integrallari

ratsional trigonometrik funksiyalarning integrallaridir. Shuning uchun, oldingi bobda ko'rsatilgan usullar ularga nisbatan qo'llanilishi mumkin. Bunday integrallarning o'ziga xos xususiyatlariga asoslangan usullar quyida muhokama qilinadi.

Agar m va n ratsional sonlar bo'lsa, u holda almashtirishlardan biri t = gunoh x yoki t = chunki x integral differensial binomning integraliga keltiriladi.

Agar m va n butun sonlar bo'lsa, u holda integratsiya kamaytirish formulalari yordamida amalga oshiriladi:

;
;
;
.

Misol:
.

Ko'phad va sinus yoki kosinus ko'paytmasining integrallari

Shaklning integrallari:
, ,
Bu erda P(x) x dagi ko'phad bo'lib, qismlar bilan integrallanadi. Bu quyidagi formulalarni beradi:

;
.

Misollar:
, .

Ko‘p nomli, ko‘rsatkichli va sinus yoki kosinus ko‘paytmasining integrallari

Shaklning integrallari:
, ,
Bu yerda P(x) Eyler formulasi yordamida integrallangan x dagi ko‘phaddir
e iax = cos ax + isin ax(bu erda i 2 = - 1 ).
Buning uchun oldingi paragrafda ko'rsatilgan usuldan foydalanib, integralni hisoblang
.
Natijadan haqiqiy va xayoliy qismlarni ajratib, asl integrallar olinadi.

Misol:
.

Trigonometrik funksiyalarni integrallashning nostandart usullari

Quyida trigonometrik funktsiyalarni birlashtirishni bajarish yoki soddalashtirish imkonini beruvchi bir qator nostandart usullar keltirilgan.

(a sin x + b cos x) ga bog'liqlik

Agar integral faqat a ga bog'liq bo'lsa sin x + b cos x, keyin formulani qo'llash foydali bo'ladi:
,
Qayerda.

Masalan

Kasrlarni sinuslar va kosinuslardan oddiy kasrlarga echish

Integralni ko'rib chiqing
.
Integratsiyaning eng oddiy usuli - bu o'zgartirish yordamida kasrni oddiyroqlarga ajratish:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Birinchi darajali integral kasrlar

Integralni hisoblashda
,
kasrning butun qismini va maxrajning hosilasini ajratib olish qulay
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)' .
A va B konstantalari chap va o'ng tomonlarini solishtirish orqali topiladi.

Adabiyotlar:
N.M. Gyunter, R.O. Kuzmin, Oliy matematika bo'yicha muammolar to'plami, "Lan", 2003 yil.

Shuningdek qarang:

R(sin x, cos x) ko`rinishdagi ratsional funksiyalarni integrallash uchun universal trigonometrik almashtirish deb ataladigan almashtirish qo`llaniladi. Keyin. Universal trigonometrik almashtirish ko'pincha katta hisob-kitoblarga olib keladi. Shuning uchun, iloji bo'lsa, quyidagi almashtirishlardan foydalaning.

Trigonometrik funktsiyalarga ratsional bog'liq bo'lgan funktsiyalarni integrallash

1. ∫ sin n xdx , ∫ cos n xdx ko‘rinishdagi integrallar. n>0
a) Agar n toq bo'lsa, differensial belgisi ostida sinx (yoki cosx) ning bir darajasi kiritilib, qolgan juftlikdan qarama-qarshi funktsiyaga o'tkazilishi kerak.
b) Agar n juft bo'lsa, darajani kamaytirish uchun formulalardan foydalanamiz
2. ∫ tg n xdx , ∫ ctg n xdx ko'rinishdagi integrallar, bunda n butun son.
Formulalardan foydalanish kerak

3. ∫ sin n x cos m x dx ko‘rinishdagi integrallar
a) m va n turli paritetlarga ega bo‘lsin. Agar n toq bo'lsa, t=sin x, m toq bo'lsa, t=cos x almashtirishdan foydalanamiz.
b) m va n juft bo'lsa, darajani kamaytirish uchun formulalardan foydalanamiz
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Shaklning integrallari
Agar m va n sonlar bir xil paritetga ega bo‘lsa, u holda t=tg x almashtirishdan foydalanamiz. Ko'pincha trigonometrik birlik texnikasidan foydalanish qulay.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Trigonometrik funktsiyalarning ko'paytmasini ularning yig'indisiga aylantirish uchun formulalardan foydalanamiz:

• sin a cos b = ½(sin(a+b)+sin(a-b))
• cos a cos b = ½(cos(a+b)+cos(a-b))
• sin a sin b = ½(cos(a-b)-cos(a+b))

Misollar
1. ∫ cos 4 x·sin 3 xdx integralini hisoblang.
Cos(x)=t almashtirishni qilamiz. U holda ∫ cos 4 x sin 3 xdx =
2. Integralni hisoblang.
Sin x=t ni almashtirsak, olamiz

3. Integralni toping.
tg(x)=t almashtirishni qilamiz. O'rnini bosamiz, biz olamiz

R(sinx, cosx) shaklidagi integral ifodalar

Misol № 1. Integrallarni hisoblang:

Yechim.
a) R(sinx, cosx) ko’rinishdagi ifodalarni integrallash, bunda R sin x va cos x ning ratsional funksiyasi tg(x/2) = t universal trigonometrik almashtirish yordamida ratsional funksiyalarning integrallariga aylantiriladi.
Keyin bizda bor

Umumjahon trigonometrik almashtirish ∫ R(sinx, cosx) dx ko'rinishdagi integraldan kasr ratsional funktsiyaning integraliga o'tish imkonini beradi, lekin ko'pincha bunday almashtirish noqulay ifodalarga olib keladi. Muayyan sharoitlarda oddiyroq almashtirishlar samarali bo'ladi:

• Agar R(-sin x, cos x) = -R(sin x, cos x)dx tengligi bajarilsa, u holda cos x = t almashtirish qo‘llaniladi.
• Agar R(sin x, -cos x) = -R(sin x, cos x)dx tenglik bajarilsa, sin x = t almashtirish.
• Agar R(-sin x, -cos x) = R(sin x, cos x)dx tengligi bajarilsa, u holda almashtirish tgx = t yoki ctg x = t bo'ladi.

Bunday holda, integralni topish uchun
tg(x/2) = t universal trigonometrik almashtirishni qo'llaymiz.
Keyin Javob:

Integrallarning qismlar bo'yicha yechimlari misollari batafsil ko'rib chiqiladi, ularning integrali ko'rsatkichli ko'rsatkichga (e ga x darajaga) yoki sinusga (sin x) yoki kosinusga (cos x) ko'paytiriladi.

Tarkib

Shuningdek qarang: Qismlar bo'yicha integratsiya usuli
Noaniq integrallar jadvali
Noaniq integrallarni hisoblash usullari
Asosiy elementar funksiyalar va ularning xossalari

Qismlar bo'yicha integratsiya formulasi

Ushbu bo'limdagi misollarni echishda qismlar bo'yicha integratsiya formulasi qo'llaniladi:
;
.

Ko'phad va sin x, cos x yoki e x ko'paytmasini o'z ichiga olgan integrallarga misollar

Mana shunday integrallarga misollar:
, , .

Bunday integrallarni integrallash uchun ko‘phad u bilan, qolgan qismi esa v dx bilan belgilanadi. Keyinchalik, qismlar bo'yicha integratsiya formulasini qo'llang.

Quyida ushbu misollarning batafsil yechimi keltirilgan.

Integrallarni yechishga misollar

X ning kuchiga e ko'rsatkichli misol

Integralni aniqlang:
.

Differensial belgisi ostida ko'rsatkichni kiritamiz:
e - x dx = - e - x d(-x) = - d(e - x).

Keling, qismlar bo'yicha birlashaylik.

Bu yerga
.
Qolgan integralni qismlar bo'yicha ham birlashtiramiz.
.
.
.
Nihoyat bizda:
.

Sinus bilan integralni aniqlashga misol

Integralni hisoblang:
.

Differensial belgisi ostida sinusni kiritamiz:

Keling, qismlar bo'yicha birlashaylik.

bu yerda u = x 2, v = cos(2 x+3), du = ( x 2 )′ dx

Qolgan integralni qismlar bo'yicha ham birlashtiramiz. Buning uchun differensial belgisi ostida kosinus kiritiladi.


bu yerda u = x, v = gunoh (2 x+3), du = dx

Nihoyat bizda:

Ko'phad va kosinus ko'paytmasiga misol

Integralni hisoblang:
.

Differensial belgisi ostida kosinusni kiritamiz:

Keling, qismlar bo'yicha birlashaylik.

bu erda u = x 2 + 3 x + 5, v = gunoh 2 x, du = ( x 2 + 3 x + 5 )′ dx

Shuningdek, siz o'zingiz hal qilishingiz kerak bo'lgan muammolar bo'ladi, ularga javoblarni ko'rishingiz mumkin.

Integratsiyani trigonometrik funktsiyalarning ko'paytmasidan yig'indiga aylantirish mumkin

X ning birinchi darajali sinuslari va kosinuslarining ko'paytmasi bo'lgan integrallarni, ya'ni ko'rinishdagi integrallarni ko'rib chiqaylik.

Taniqli trigonometrik formulalardan foydalanish

(2)
(3)
(4)
(31) ko'rinishdagi integrallarning har birini algebraik yig'indiga aylantirish va formulalar bo'yicha integrallash mumkin.

(5)

(6)

1-misol. Toping

Yechim. Formulaga muvofiq (2) da

2-misol. Toping trigonometrik funktsiyaning integrali

Yechim. Formulaga muvofiq (3) da

3-misol. Toping trigonometrik funktsiyaning integrali

Yechim. Formulaga muvofiq (4) da biz integralning quyidagi o'zgarishini olamiz:

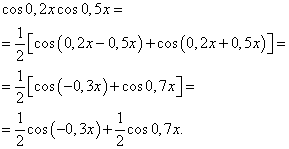
Formulani (6) qo'llash orqali biz olamiz

Xuddi shu argumentning sinus va kosinus darajalari hosilasining integrali

Keling, bir xil argumentning sinus va kosinus darajalarining mahsuloti bo'lgan funktsiyalarning integrallarini ko'rib chiqaylik, ya'ni.

(7)

Maxsus holatlarda ko'rsatkichlardan biri ( m yoki n) nolga teng bo'lishi mumkin.

Bunday funktsiyalarni integrallashda kosinusning teng kuchi sinus orqali ifodalanishi mumkinligi va sinusning differensialligi cos ga teng ekanligidan foydalaniladi. x dx(yoki hatto sinusning kuchini kosinus bilan ifodalash mumkin va kosinusning differentsiali - singa teng. x dx ) .

Ikkita holatni ajratib ko'rsatish kerak: 1) ko'rsatkichlardan kamida bittasi m Va n g'alati; 2) ikkala ko'rsatkich ham juft.

Birinchi holat sodir bo'lsin, ya'ni indikator n = 2k+ 1 - g'alati. Keyin, shuni hisobga olgan holda

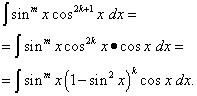
Integrasiya shunday berilganki, uning bir qismi faqat sinusning funksiyasi, ikkinchisi esa sinusning differensial qismidir. Endi o'zgaruvchan almashtirishdan foydalaning t= gunoh x yechim ko'phadni ga nisbatan integrallashga qisqartiradi t. Agar faqat daraja bo'lsa m g'alati bo'lsa, ular ham xuddi shunday qilishadi, omil gunohni ajratib turadilar x, integrandning qolgan qismini cos bilan ifodalaydi x va ishonish t=cos x. Ushbu texnikani qachon ham qo'llash mumkin sinus va kosinusning nisbat kuchlarini birlashtirish , Qachon ko'rsatkichlardan kamida bittasi toq . Gap shundaki sinus va kosinus kuchlarining nisbati ularning mahsulotining alohida holatidir : Trigonometrik funktsiya integralning maxrajida bo'lsa, uning darajasi manfiy bo'ladi. Ammo qisman trigonometrik funktsiyalarning kuchlari faqat juft bo'lgan holatlar ham mavjud. Ular haqida - keyingi xatboshida.

Agar ikkala ko'rsatkich bo'lsa m Va n– hatto, keyin, trigonometrik formulalar yordamida

sinus va kosinusning ko'rsatkichlarini kamaytiring, shundan so'ng yuqoridagi kabi bir xil turdagi integral olinadi. Shuning uchun integratsiyani xuddi shu sxema bo'yicha davom ettirish kerak. Agar juft ko'rsatkichlardan biri manfiy bo'lsa, ya'ni sinus va kosinusning juft darajalari nisbati hisobga olinsa, bu sxema mos kelmaydi. . Keyin o'zgaruvchining o'zgarishi integralni qanday o'zgartirish mumkinligiga qarab ishlatiladi. Bunday holat keyingi bandda ko'rib chiqiladi.

4-misol. Toping trigonometrik funktsiyaning integrali

Yechim. Kosinus ko'rsatkichi g'alati. Shuning uchun, keling, tasavvur qilaylik

t= gunoh x(Keyin dt=cos x dx ). Keyin olamiz

Eski o'zgaruvchiga qaytsak, biz nihoyat topamiz

5-misol. Toping trigonometrik funktsiyaning integrali

.

Yechim. Kosinus ko'rsatkichi, oldingi misolda bo'lgani kabi, g'alati, lekin kattaroqdir. Tasavvur qilaylik

va o'zgaruvchini o'zgartirish t= gunoh x(Keyin dt=cos x dx ). Keyin olamiz

Qavslarni ochamiz

va biz olamiz

Eski o'zgaruvchiga qaytsak, biz yechimni olamiz

6-misol. Toping trigonometrik funktsiyaning integrali

Yechim. Sinus va kosinusning darajalari juft. Shunday qilib, integral funktsiyani quyidagicha o'zgartiramiz:

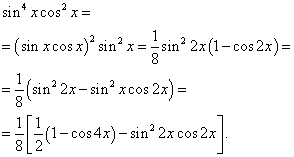
Keyin olamiz

Ikkinchi integralda biz o'zgaruvchini o'zgartiramiz, sozlash t= gunoh2 x. Keyin (1/2)dt= cos2 x dx . Demak,

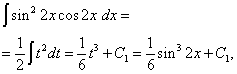
Nihoyat, olamiz

O'zgaruvchilarni almashtirish usulidan foydalanish

O'zgaruvchilarni almashtirish usuli trigonometrik funksiyalarni integrallashda u integranda faqat sinus yoki faqat kosinus, sinus va kosinusning ko‘paytmasi bo‘lgan, sinus yoki kosinus birinchi darajali, tangens yoki kotangens, shuningdek, ko‘rsatkich bo‘lgan hollarda qo‘llanilishi mumkin. hatto bir va bir xil argumentning sinus va kosinus kuchlari. Bunday holda, faqat gunoh emas, balki almashtirishni amalga oshirish mumkin x = t va gunoh x = t, balki tg x = t va ctg x = t .

8-misol. Toping trigonometrik funktsiyaning integrali

.

Yechim. O'zgaruvchini o'zgartiramiz: , keyin . Olingan integralni integrallar jadvali yordamida osongina integrallash mumkin:

.

9-misol. Toping trigonometrik funktsiyaning integrali

Yechim. Tangensni sinus va kosinus nisbatiga aylantiramiz:

O'zgaruvchini o'zgartiramiz: , keyin . Olingan integral jadval integrali minus belgisi bilan:

.

Asl o'zgaruvchiga qaytsak, biz nihoyat quyidagilarni olamiz:

.

10-misol. Toping trigonometrik funktsiyaning integrali

Yechim. O'zgaruvchini o'zgartiramiz: , keyin .

Trigonometrik identifikatsiyani qo'llash uchun integralni o'zgartiramiz :

Biz o'zgaruvchini o'zgartiramiz, integral oldiga minus belgisini qo'yishni unutmang (yuqoriga qarang, nimaga teng dt). Keyinchalik, biz integratsiyani faktorlarga ajratamiz va jadvalga muvofiq integrallaymiz:

Asl o'zgaruvchiga qaytsak, biz nihoyat quyidagilarni olamiz:

.

Trigonometrik funktsiyaning integralini o'zingiz toping va keyin yechimga qarang

Universal trigonometrik almashtirish

Universal trigonometrik almashtirish integrand oldingi bandlarda ko'rib chiqilgan holatlarga kirmaydigan hollarda qo'llanilishi mumkin. Asosan, sinus yoki kosinus (yoki ikkalasi) kasrning maxrajida bo'lganda. Sinus va kosinusni asl burchakning yarmi tangensini o'z ichiga olgan boshqa ifoda bilan quyidagi tarzda almashtirish mumkinligi isbotlangan:

Ammo shuni yodda tutingki, universal trigonometrik almashtirish ko'pincha juda murakkab algebraik o'zgarishlarni o'z ichiga oladi, shuning uchun boshqa hech qanday usul ishlamasa, uni ishlatish yaxshiroqdir. Keling, universal trigonometrik almashtirish bilan birgalikda differentsial belgi ostida almashtirish va noaniq koeffitsientlar usuli qo'llaniladigan misollarni ko'rib chiqaylik.

12-misol. Toping trigonometrik funktsiyaning integrali

.

Yechim. Yechim. Keling, foyda keltiraylik universal trigonometrik almashtirish. Keyin
.

Numerator va maxrajdagi kasrlarni ga ko'paytiramiz va ikkitasini chiqarib, integral belgisi oldiga qo'yamiz. Keyin

Amalda ko'pincha trigonometrik funktsiyalarni o'z ichiga olgan transsendental funktsiyalarning integrallarini hisoblash kerak bo'ladi. Ushbu materialning bir qismi sifatida biz integral funktsiyalarning asosiy turlarini tavsiflaymiz va ularni birlashtirish uchun qanday usullardan foydalanish mumkinligini ko'rsatamiz.

Sinus, kosinus, tangens va kotangensni integrallash

Keling, asosiy trigonometrik funktsiyalarni integrallash usullaridan boshlaylik - sin, cos, t g, c t g. Antiderivativlar jadvalidan foydalanib, darhol ∫ sin x d x = - cos x + C, va ∫ cos x d x = sin x + C ekanligini yozamiz.

t g va c t g funktsiyalarining noaniq integrallarini hisoblash uchun siz differentsial belgidan foydalanishingiz mumkin:

∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C

Antiderivativlar jadvalidan olingan ∫ d x sin x = ln 1 - cos x sin x + C va ∫ d x cos x = ln 1 + sin x cos x + C formulalarini qanday oldik? Keling, faqat bitta holatni tushuntiramiz, chunki ikkinchisi o'xshashlik bilan aniq bo'ladi.

O'zgartirish usulidan foydalanib, biz yozamiz:

∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Bu erda biz irratsional funktsiyani integrallashimiz kerak. Biz bir xil almashtirish usulidan foydalanamiz:

∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 1 - z 2 = = 1 - z ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

Endi biz teskari almashtirishni amalga oshiramiz z = 1 - t 2 va t = sin x:

∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x kabi trigonometrik funksiyalarning darajalari bo‘lgan integralli holatlarni alohida tahlil qilamiz.

Ularni qanday qilib to'g'ri hisoblash haqida takrorlash formulalari yordamida integratsiyaga oid maqolada o'qishingiz mumkin. Agar siz bu formulalar qanday olinganligini bilsangiz, ∫ sin n x · cos m x d x kabi integrallarni natural m va n bilan osongina olishingiz mumkin.

Agar bizda trigonometrik funktsiyalarning polinomlar yoki eksponensial funktsiyalar bilan kombinatsiyasi bo'lsa, ular qismlar bilan integrallanishi kerak bo'ladi. ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a integrallarini topish usullariga bag'ishlangan maqolani o'qishni tavsiya qilamiz. · x · cos (a x) d x .

Eng qiyin masalalar - bu integral turli argumentlarga ega bo'lgan trigonometrik funktsiyalarni o'z ichiga olgan masalalardir. Buni amalga oshirish uchun siz asosiy trigonometriya formulalaridan foydalanishingiz kerak, shuning uchun ularni eslab qolish yoki ularni qo'lda yozib olish tavsiya etiladi.

1-misol

y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) funksiyaning anti hosilalari toʻplamini toping.

Yechim

Darajani kamaytirish formulalaridan foydalanamiz va cos 2 x 2 = 1 + cos x 2 va cos 2 2 x = 1 + cos 4 x 2 ekanligini yozamiz. Ma'nosi,

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)

Maxrajda yig'indining sinusi formulasi mavjud. Keyin uni quyidagicha yozishingiz mumkin:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)

Biz 3 ta integralning yig'indisini oldik.

∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

Ayrim hollarda integral ostidagi trigonometrik funksiyalarni standart almashtirish usuli yordamida kasrli ratsional ifodalarga keltirish mumkin. Birinchidan, sin, cos va t g ni yarim argumentning tangensi orqali ifodalovchi formulalarni olaylik:

sin x = 2 t g x 2 1 + t g 2 x 2, sin x = 1 - t g 2 x 2 1 + t g 2 x 2, t g x = 2 t g x 2 1 - t g 2 x 2

Shuningdek, d x differensialini yarim burchakning tangensi bilan ifodalashimiz kerak bo'ladi:

d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2 bo'lgani uchun

d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

Shunday qilib, sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x = 2 d z 1 + z 2 at z = t g x 2.

2-misol

∫ d x 2 sin x + cos x + 2 noaniq integralni toping.

Yechim

Biz standart trigonometrik almashtirish usulidan foydalanamiz.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3

∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 ekanligini olamiz.

Endi biz integralni oddiy kasrlarga kengaytira olamiz va ikkita integral yig'indisini olamiz:

∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = l z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Javob: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

Shuni ta'kidlash kerakki, funktsiyalarni yarim argumentning tangensi orqali ifodalovchi formulalar bir xillik emas, shuning uchun ln t g x 2 + 1 t g x 2 + 3 + C ifodasi y = 1 2 funktsiyaning antiderivativlari to'plamidir. sin x + cos x + 2 faqat ta'rif sohasida.

Boshqa turdagi muammolarni hal qilish uchun siz asosiy integratsiya usullaridan foydalanishingiz mumkin.

Agar siz matnda xatolikni sezsangiz, uni belgilang va Ctrl+Enter tugmalarini bosing