Całkowanie funkcji trygonometrycznych. Całkowanie funkcji trygonometrycznych: metody i przykłady rozwiązywania całek trygonometrycznych

Przedstawiono podstawowe wzory trygonometryczne i podstawowe podstawienia. Omówiono metody całkowania funkcji trygonometrycznych - całkowanie funkcji wymiernych, iloczyn funkcji potęgowych sin x i cos x, iloczyn wielomianu, wykładniczego i sinusa lub cosinusa, całkowanie odwrotnych funkcji trygonometrycznych. Dotyczy to metod niestandardowych.

Treść

Standardowe metody całkowania funkcji trygonometrycznych

Ogólne podejście

Najpierw, jeśli to konieczne, całkę należy przekształcić tak, aby funkcje trygonometryczne zależały od jednego argumentu, który jest taki sam jak zmienna całkująca.

Na przykład, jeśli całka zależy od grzech(x+a) I cos(x+b), to powinieneś wykonać konwersję:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + grzech ( x+a ) grzech (b-a).
Następnie dokonaj zamiany z = x+a. W rezultacie funkcje trygonometryczne będą zależeć tylko od zmiennej całkującej z.

Gdy funkcje trygonometryczne zależą od jednego argumentu, który pokrywa się ze zmienną całkującą (powiedzmy, że jest to z), to znaczy, że całka składa się tylko z funkcji takich jak grzech z, bo z, tg z, ctg z, to musisz dokonać zamiany
.
Takie podstawienie prowadzi do całkowania funkcji wymiernych lub niewymiernych (jeśli istnieją pierwiastki) i pozwala obliczyć całkę, jeśli jest ona zintegrowana z funkcjami elementarnymi.

Często jednak można znaleźć inne metody, które pozwalają oszacować całkę w krótszy sposób, w oparciu o specyfikę całki. Poniżej znajduje się podsumowanie głównych takich metod.

Metody całkowania funkcji wymiernych sin x i cos x

Funkcje wymierne z grzech x I bo x są funkcjami utworzonymi z grzech x, bo x oraz dowolne stałe wykorzystujące operacje dodawania, odejmowania, mnożenia, dzielenia i podnoszenia do potęgi całkowitej. Są one oznaczone następująco: R (grzech x, cos x). Może to również obejmować styczne i cotangensy, ponieważ powstają one poprzez podzielenie sinusa przez cosinus i odwrotnie.
Całki funkcji wymiernych mają postać:
.

Metody całkowania wymiernych funkcji trygonometrycznych są następujące.
1) Podstawienie zawsze prowadzi do całki ułamka wymiernego. Jednak w niektórych przypadkach zdarzają się podstawienia (przedstawione poniżej), które prowadzą do krótszych obliczeń.
2) Jeżeli R (grzech x, cos x) cos x → - cos x grzech x.
3) Jeżeli R (grzech x, cos x) pomnożona przez -1 podczas zastępowania grzech x → - grzech x, wówczas podstawienie t = bo x.
4) Jeżeli R (grzech x, cos x) nie zmienia się jak w przypadku jednoczesnej wymiany cos x → - cos x, I grzech x → - grzech x, wówczas podstawienie t = tg x lub t = ctg x.

Przykłady:
, , .

Iloczyn funkcji potęgowych cos x i sin x

Całki postaci

są całkami wymiernych funkcji trygonometrycznych. Dlatego można do nich zastosować metody opisane w poprzedniej sekcji. Metody oparte na specyfice takich całek omówiono poniżej.

Jeśli m i n są liczbami wymiernymi, to jedno z podstawień t = grzech x lub t = bo x całka jest zredukowana do całki z dwumianu różniczkowego.

Jeśli m i n są liczbami całkowitymi, całkowanie przeprowadza się za pomocą wzorów redukcyjnych:

;
;
;
.

Przykład:
.

Całki iloczynu wielomianu oraz sinus lub cosinus

Całki postaci:
, ,
gdzie P(x) jest wielomianem w x, są całkowane przez części. Daje to następujące formuły:

;
.

Przykłady:
, .

Całki iloczynu wielomianu, wykładnicze i sinus lub cosinus

Całki postaci:
, ,
gdzie P(x) jest wielomianem w x całkowanym za pomocą wzoru Eulera
e iax = topór cos + topór isin(gdzie i 2 = - 1 ).
Aby to zrobić, korzystając z metody opisanej w poprzednim akapicie, oblicz całkę
.
Oddzielając część rzeczywistą i urojoną od wyniku, otrzymuje się całki pierwotne.

Przykład:
.

Niestandardowe metody całkowania funkcji trygonometrycznych

Poniżej znajduje się szereg niestandardowych metod, które pozwalają wykonać lub uprościć całkowanie funkcji trygonometrycznych.

Zależność od (a grzech x + b cos x)

Jeśli całka zależy tylko od a grzech x + b cos x, wówczas warto zastosować wzór:
,
Gdzie .

Na przykład

Rozdzielanie ułamków sinusów i cosinusów na prostsze ułamki zwykłe

Rozważ całkę
.
Najprostszą metodą całkowania jest rozbicie ułamka na prostsze za pomocą transformacji:
grzech(a - b) = grzech(x + a - (x + b)) = grzech(x+a) cos(x+b) - cos(x+a) grzech(x+b)

Całkowanie ułamków pierwszego stopnia

Przy obliczaniu całki
,
wygodnie jest odizolować część całkowitą ułamka i pochodną mianownika
A 1 grzech x + b 1 cos x = A (a grzech x + b cos x) + B (a grzech x + b cos x)′ .
Stałe A i B można znaleźć porównując lewą i prawą stronę.

Bibliografia:
N.M. Gunter, RO Kuźmin, Zbiór problemów matematyki wyższej, „Lan”, 2003.

Zobacz też:

Do całkowania funkcji wymiernych postaci R(sin x, cos x) stosuje się podstawienie, które nazywa się uniwersalnym podstawieniem trygonometrycznym. Następnie . Uniwersalne podstawienie trygonometryczne często skutkuje dużymi obliczeniami. Dlatego, jeśli to możliwe, użyj następujących podstawień.

Całkowanie funkcji wymiernie zależnych od funkcji trygonometrycznych

1. Całki postaci ∫ sin n xdx , ∫ cos n xdx , n>0
a) Jeżeli n jest nieparzyste, to pod znak różniczki należy wpisać jedną potęgę sinx (lub cosx), a z pozostałej potęgi parzystej przekazać funkcję przeciwną.
b) Jeżeli n jest parzyste, to stosujemy wzory na redukcję stopnia
2. Całki postaci ∫ tg n xdx , ∫ ctg n xdx , gdzie n jest liczbą całkowitą.
Należy używać formuł

3. Całki postaci ∫ sin n x cos m x dx
a) Niech m i n będą miały różne parzystości. Używamy podstawienia t=sin x, jeśli n jest nieparzyste lub t=cos x, jeśli m jest nieparzyste.
b) Jeśli m i n są parzyste, wówczas używamy wzorów na redukcję stopnia
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Całki postaci
Jeśli liczby m i n mają tę samą parzystość, wówczas stosujemy podstawienie t=tg x. Często wygodnie jest zastosować technikę jednostek trygonometrycznych.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Skorzystajmy ze wzorów na przeliczenie iloczynu funkcji trygonometrycznych na ich sumę:

• grzech α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• grzech α grzech β = ½(cos(α-β)-cos(α+β))

Przykłady
1. Oblicz całkę ∫ cos 4 x·sin 3 xdx .
Dokonujemy zamiany cos(x)=t. Wtedy ∫ cos 4 x sin 3 xdx =
2. Oblicz całkę.
Dokonując zamiany sin x=t , otrzymujemy

3. Znajdź całkę.
Dokonujemy zamiany tg(x)=t . Podstawiając, otrzymujemy

Całkowanie wyrażeń w postaci R(sinx, cosx)

Przykład nr 1. Oblicz całki:

Rozwiązanie.
a) Całkowanie wyrażeń w postaci R(sinx, cosx), gdzie R jest funkcją wymierną sin x i cos x, przekształcamy na całki funkcji wymiernych przy użyciu uniwersalnego podstawienia trygonometrycznego tg(x/2) = t.
Następnie mamy

Uniwersalne podstawienie trygonometryczne umożliwia przejście od całki postaci ∫ R(sinx, cosx) dx do całki ułamkowej funkcji wymiernej, jednak często takie podstawienie prowadzi do uciążliwych wyrażeń. W pewnych warunkach skuteczne są prostsze podstawienia:

• Jeżeli spełniona jest równość R(-sin x, cos x) = -R(sin x, cos x)dx, wówczas stosuje się podstawienie cos x = t.
• Jeżeli zachodzi równość R(sin x, -cos x) = -R(sin x, cos x)dx, to podstawienie sin x = t.
• Jeżeli zachodzi równość R(-sin x, -cos x) = R(sin x, cos x)dx, to podstawienie tgx = t lub ctg x = t.

W tym przypadku, aby znaleźć całkę
zastosujmy uniwersalne podstawienie trygonometryczne tg(x/2) = t.
Następnie odpowiedz:

Szczegółowo rozważono przykłady rozwiązań całek przez części, których całka jest iloczynem wielomianu przez wykładnik (e do potęgi x) lub przez sinus (sin x) lub cosinus (cos x).

Treść

Zobacz też: Metoda całkowania przez części
Tabela całek nieoznaczonych
Metody obliczania całek nieoznaczonych
Podstawowe funkcje elementarne i ich własności

Wzór na całkowanie przez części

Podczas rozwiązywania przykładów w tej sekcji używana jest formuła całkowania przez części:
;
.

Przykłady całek zawierających iloczyn wielomianu i sin x, cos x lub ex

Oto przykłady takich całek:
, , .

Aby całkować takie całki, wielomian oznacza się przez u, a pozostałą część przez v dx. Następnie zastosuj formułę całkowania przez części.

Poniżej znajduje się szczegółowe rozwiązanie tych przykładów.

Przykłady rozwiązywania całek

Przykład z wykładnikiem e do potęgi x

Wyznacz całkę:
.

Wprowadźmy wykładnik pod znakiem różniczkowym:
e - x dx = - e - x d(-x) = - d(e - x).

Całkujmy przez części.

Tutaj
.
Całkujemy również pozostałą całkę przez części.
.
.
.
Wreszcie mamy:
.

Przykład zdefiniowania całki z sinusem

Oblicz całkę:
.

Wprowadźmy sinus pod znakiem różniczkowym:

Całkujmy przez części.

tutaj u = x 2 , v = cos(2x+3), du = ( x 2 )′ dx

Całkujemy również pozostałą całkę przez części. Aby to zrobić, wprowadź cosinus pod znakiem różniczkowym.


tutaj u = x, v = grzech(2 x+3), du = dx

Wreszcie mamy:

Przykład iloczynu wielomianu i cosinusa

Oblicz całkę:
.

Wprowadźmy cosinus pod znakiem różniczkowym:

Całkujmy przez części.

tutaj u = x 2 + 3 x + 5, v = grzech 2x, du = ( x 2 + 3 x + 5 )′ dx

Pojawią się także problemy do samodzielnego rozwiązania, na które możesz zobaczyć odpowiedzi.

Całkę można przekształcić z iloczynu funkcji trygonometrycznych na sumę

Rozważmy całki, w których całka jest iloczynem sinusów i cosinusów pierwszego stopnia x pomnożonych przez różne czynniki, czyli całki postaci

Korzystanie ze znanych wzorów trygonometrycznych

(2)
(3)
(4)
każdy z iloczynów można przekształcić w całki postaci (31) na sumę algebraiczną i całkować według wzorów

(5)

(6)

Przykład 1. Znajdować

Rozwiązanie. Według wzoru (2) o godz

Przykład 2. Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Według wzoru (3) przy

Przykład 3. Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Według wzoru (4) przy otrzymujemy następującą transformację całki:

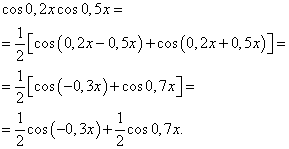
Stosując wzór (6) otrzymujemy

Całka iloczynu potęg sinusa i cosinusa tego samego argumentu

Rozważmy teraz całki funkcji, które są iloczynem potęg sinusa i cosinusa tego samego argumentu, tj.

(7)

W szczególnych przypadkach jeden ze wskaźników ( M Lub N) może wynosić zero.

Przy całkowaniu takich funkcji przyjmuje się, że parzystą potęgę cosinusa można wyrazić za pomocą sinusa, a różniczka sinusa jest równa cos x dx(lub nawet potęgę sinusa można wyrazić w postaci cosinusa, a różniczka cosinusa jest równa - grzech x dx ) .

Należy rozróżnić dwa przypadki: 1) co najmniej jeden ze wskaźników M I N dziwne; 2) oba wskaźniki są równe.

Niech zajdzie pierwszy przypadek, a mianowicie wskaźnik N = 2k+ 1 - dziwne. Biorąc to pod uwagę

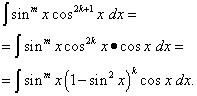
Całkę przedstawia się w ten sposób, że jedna jej część jest funkcją tylko sinusa, a druga jest różniczką sinusa. Teraz używam zamiany zmiennych T= grzech X rozwiązanie sprowadza się do całkowania wielomianu względem T. Jeśli tylko stopień M jest dziwne, wówczas robią to samo, izolując czynnik grzech X, wyrażając resztę całki w postaci cos X i wierząc T=co X. Technikę tę można również zastosować, gdy całkowanie potęg ilorazu sinusa i cosinusa , Gdy przynajmniej jeden ze wskaźników jest nieparzysty . Cały sens w tym iloraz potęg sinusa i cosinusa jest szczególnym przypadkiem ich iloczynu : Gdy funkcja trygonometryczna znajduje się w mianowniku całki, jej stopień jest ujemny. Ale zdarzają się również przypadki częściowych funkcji trygonometrycznych, gdy ich potęgi są tylko parzyste. O nich – w następnym akapicie.

Jeśli oba wskaźniki M I N– nawet wtedy, używając wzorów trygonometrycznych

zmniejsz wykładniki sinusa i cosinusa, po czym otrzymasz całkę tego samego typu co powyżej. Dlatego też integracja powinna być kontynuowana według tego samego schematu. Jeśli jeden z parzystych wykładników jest ujemny, to znaczy bierze się pod uwagę iloraz parzystych potęg sinusa i cosinusa, wówczas ten schemat nie jest odpowiedni . Następnie stosuje się zmianę zmiennej w zależności od tego, w jaki sposób całka może zostać przekształcona. Taki przypadek zostanie omówiony w następnym akapicie.

Przykład 4. Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Wykładnik cosinus jest nieparzysty. Dlatego wyobraźmy sobie

T= grzech X(Następnie dt=co X dx ). Wtedy otrzymamy

Wracając do starej zmiennej, w końcu znajdujemy

Przykład 5. Znajdować całka funkcji trygonometrycznej

.

Rozwiązanie. Wykładnik cosinus, jak w poprzednim przykładzie, jest nieparzysty, ale większy. Wyobraźmy sobie

i dokonaj zmiany zmiennej T= grzech X(Następnie dt=co X dx ). Wtedy otrzymamy

Otwórzmy nawiasy

i otrzymujemy

Wracając do starej zmiennej, otrzymujemy rozwiązanie

Przykład 6. Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Wykładniki sinusa i cosinusa są parzyste. Dlatego przekształcamy funkcję całkową w następujący sposób:

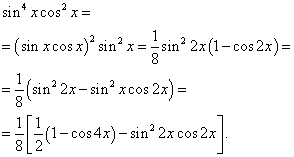
Wtedy otrzymamy

W drugiej całce dokonujemy zmiany zmiennej, ustawienie T= grzech2 X. Następnie (1/2)dt= cos2 X dx . Stąd,

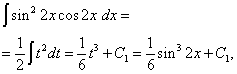
Wreszcie dostajemy

Korzystanie z metody zastępowania zmiennych

Zmienna metoda wymiany przy całkowaniu funkcji trygonometrycznych można go zastosować w przypadkach, gdy podcałka zawiera tylko sinus lub tylko cosinus, iloczyn sinusa i cosinusa, w którym sinus lub cosinus jest pierwszego stopnia, styczną lub cotangens, a także iloraz nawet potęgi sinusa i cosinusa tego samego argumentu. W tym przypadku możliwe jest wykonanie permutacji nie tylko grzechu X = T i grzech X = T, ale także tg X = T i ctg X = T .

Przykład 8. Znajdować całka funkcji trygonometrycznej

.

Rozwiązanie. Zmieńmy zmienną: , a następnie . Powstałą całkę można łatwo zintegrować, korzystając z tabeli całek:

.

Przykład 9. Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Przekształćmy tangens na stosunek sinusa i cosinusa:

Zmieńmy zmienną: , a następnie . Powstała całka to integralna tabela ze znakiem minus:

.

Wracając do pierwotnej zmiennej, w końcu otrzymujemy:

.

Przykład 10. Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Zmieńmy zmienną: , a następnie .

Przekształćmy całkę, aby zastosować tożsamość trygonometryczną :

Zmieniamy zmienną, nie zapominając o umieszczeniu znaku minus przed całką (patrz wyżej, co jest równe dt). Następnie rozkładamy całkę na czynniki i całkujemy zgodnie z tabelą:

Wracając do pierwotnej zmiennej, w końcu otrzymujemy:

.

Znajdź samodzielnie całkę funkcji trygonometrycznej, a następnie spójrz na rozwiązanie

Uniwersalne podstawienie trygonometryczne

Uniwersalne podstawienie trygonometryczne można zastosować w przypadkach, gdy całka nie wchodzi w zakres przypadków omówionych w poprzednich akapitach. Zasadniczo, gdy sinus lub cosinus (lub oba) znajdują się w mianowniku ułamka. Udowodniono, że sinus i cosinus można zastąpić innym wyrażeniem zawierającym tangens połowy pierwotnego kąta w następujący sposób:

Należy jednak pamiętać, że uniwersalne podstawienie trygonometryczne często pociąga za sobą dość złożone przekształcenia algebraiczne, dlatego najlepiej go stosować, gdy żadna inna metoda nie zadziała. Przyjrzyjmy się przykładom, gdzie obok uniwersalnego podstawienia trygonometrycznego stosuje się podstawienie pod znakiem różniczkowym i metodę współczynników nieokreślonych.

Przykład 12. Znajdować całka funkcji trygonometrycznej

.

Rozwiązanie. Rozwiązanie. Skorzystajmy uniwersalne podstawienie trygonometryczne. Następnie
.

Mnożymy ułamki w liczniku i mianowniku przez , usuwamy te dwa i umieszczamy przed znakiem całki. Następnie

W praktyce często konieczne jest obliczenie całek funkcji przestępnych zawierających funkcje trygonometryczne. W ramach tego materiału opiszemy główne typy funkcji całkowych i pokażemy, jakimi metodami można je zintegrować.

Całkowanie sinusa, cosinusa, tangensa i cotangensa

Zacznijmy od metod całkowania podstawowych funkcji trygonometrycznych – sin, cos, t g, c t g. Korzystając z tabeli funkcji pierwotnych, od razu piszemy, że ∫ sin x d x = - cos x + C i ∫ cos x d x = sin x + C.

Aby obliczyć całki nieoznaczone funkcji t g i c t g, możesz użyć znaku różniczkowego:

∫ t sol x re x = ∫ grzech x cos x re x = d (cos x) = - grzech x re x = = - ∫ d (cos x) cos x = - ln cos x + do ∫ do t g x re x = ∫ sałata x grzech x d x = d (grzech x) = sałata x re x = = ∫ re (grzech x) grzech x = ln grzech x + C

Jak otrzymaliśmy wzory ∫ d x sin x = ln 1 - cos x sin x + C i ∫ d x cos x = ln 1 + sin x cos x + C, wzięte z tabeli funkcji pierwotnych? Wyjaśnijmy tylko jeden przypadek, drugi bowiem będzie jasny przez analogię.

Stosując metodę podstawieniową piszemy:

∫ re x grzech x = grzech x = t ⇒ x = za r do grzech y ⇒ re x = re t 1 - t 2 = re t t 1 - t 2

Tutaj musimy zintegrować funkcję niewymierną. Używamy tej samej metody podstawienia:

∫ re t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ re t = - z re z 1 - z 2 = = ∫ - z re z z 1 - z 2 1 - z 2 = ∫ re z z 2 - 1 = ∫ re z (z - 1) (z +) = = 1 2 ∫ re z z - 1 - 1 2 ∫ re z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + do = = 1 2 ln z - 1 z + 1 + do = ln z - 1 z + 1 + do

Teraz dokonujemy odwrotnego podstawienia z = 1 - t 2 i t = sin x:

∫ re x grzech x = ∫ re t t 1 - t 2 = ln z - 1 z + 1 + do = = ln 1 - t 2 - 1 1 - t 2 + 1 + do = ln 1 - grzech 2 x - 1 1 - grzech 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 grzech 2 x + C = = ln cos x - 1 grzech x + C

Osobno przeanalizujemy przypadki z całkami zawierającymi potęgi funkcji trygonometrycznych, takie jak ∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x.

O tym, jak je poprawnie obliczyć, przeczytasz w artykule o całkowaniu za pomocą formuł rekurencyjnych. Jeśli wiesz, jak wyprowadzane są te wzory, możesz łatwo obliczyć całki takie jak ∫ sin n x · cos m x d x z naturalnymi m i n.

Jeśli mamy kombinację funkcji trygonometrycznych z wielomianami lub funkcjami wykładniczymi, wówczas będą musiały być całkowane przez części. Polecamy przeczytać artykuł poświęcony metodom znajdowania całek ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a · x · cos (a x) re x .

Najtrudniejsze są zadania, w których całka zawiera funkcje trygonometryczne z różnymi argumentami. Aby to zrobić, musisz skorzystać z podstawowych wzorów trygonometrycznych, dlatego warto je zapamiętać lub mieć pod ręką.

Przykład 1

Znajdź zbiór funkcji pierwotnych funkcji y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) .

Rozwiązanie

Skorzystajmy ze wzorów na stopień redukcji i napiszmy, że cos 2 x 2 = 1 + cos x 2 i cos 2 2 x = 1 + cos 4 x 2. Oznacza,

y = grzech (4 x) + 2 cos 2 (2 x) grzech x cos (3 x) + 2 cos 2 x 2 - 1 grzech (3 x) = grzech (4 x) + 2 1 + cos 4 x 2 grzech x cos (3 x) + 2 1 + cos x 2 - 1 grzech (3 x) = = grzech (4 x) + cos (4 x) + 1 grzech x cos (3 x) + cos x grzech (3 x)

W mianowniku mamy wzór na sinus sumy. Następnie możesz napisać to w ten sposób:

y = grzech (4 x) + cos (4 x) + 1 grzech x cos (3 x) + cos x grzech (3 x) = grzech (4 x) + cos (4 x) + 1 grzech (4 x ) = = 1 + cos (4 x) grzech (4 x)

Otrzymaliśmy sumę 3 całek.

∫ grzech (4 x) + sałata (4 x) + 1 grzech x · sałata (3 x) + cos x · grzech (3 x) re x = = ∫ re x + sałata (4 x) d x grzech (4 x) + ∫ d x grzech (4 x) = = x + 1 4 ln ∫ d (grzech (4 x)) grzech (4 x) + 1 4 ln cos (4 x) - 1 grzech (4 x) = = 1 4 ln grzech ( 4 x) + 1 4 ln cos (4 x) - 1 grzech (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

W niektórych przypadkach funkcje trygonometryczne pod całką można sprowadzić do ułamkowych wyrażeń wymiernych, stosując standardową metodę podstawienia. Najpierw weźmy formuły wyrażające grzech, cos i t g poprzez tangens argumentu połówkowego:

grzech x = 2 t sol x 2 1 + t sol 2 x 2 , grzech x = 1 - t sol 2 x 2 1 + t sol 2 x 2 , t sol x = 2 t sol x 2 1 - t sol 2 x 2

Będziemy musieli także wyrazić różnicę d x w postaci tangensa kąta połówkowego:

Ponieważ d t sol x 2 = t g x 2 "d x = d x 2 cos 2 x 2, to

re x = 2 sałata 2 x 2 re t sol x 2 = 2 re t sol x 2 1 sałata 2 x 2 = 2 re t sol x 2 sałata 2 x 2 + grzech 2 x 2 sałata 2 x 2 = 2 re t sol x 2 1 + t sol 2 x 2

Zatem sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t sol x 2 z 1 - z 2, re x = 2 re z 1 + z 2 w z = t g x 2.

Przykład 2

Znajdź całkę nieoznaczoną ∫ d x 2 sin x + cos x + 2 .

Rozwiązanie

Stosujemy metodę standardowego podstawienia trygonometrycznego.

2 grzech x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ re x 2 grzech x + cos x + 2 = 2 re z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 re z z 2 + 4 z + 3

Otrzymujemy, że ∫ re x 2 grzech x + sałata x + 2 = 2 re z z 2 + 4 z + 3 .

Teraz możemy rozwinąć całkę na ułamki proste i otrzymać sumę dwóch całek:

∫ re x 2 grzech x + sałata x + 2 = 2 ∫ 2 re z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 re z = = ∫ re z z + 1 - ∫ do z + 3 = ln z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ re x 2 grzech x + sałata x + 2 = ln z + 1 z + 3 + do = ln t sol x 2 + 1 t sol x 2 + 3 + C

Odpowiedź: ∫ re x 2 grzech x + cos x + 2 = ln t sol x 2 + 1 t sol x 2 + 3 + C

Należy zauważyć, że wzory wyrażające funkcje poprzez tangens połowy argumentu nie są tożsamościami, dlatego powstałe wyrażenie ln t g x 2 + 1 t g x 2 + 3 + C jest zbiorem funkcji pierwotnych funkcji y = 1 2 sin x + cos x + 2 tylko w dziedzinie definicji.

Aby rozwiązać inne rodzaje problemów, możesz użyć podstawowych metod integracji.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter